Pytorch实现广义回归神经网络GRNN

【悲报】这篇文章的代码没有批量预测，看了基本原理后可以移步新文章：Tensor，广播机制与GRNN重构 – KAKO Academy of Sciences (kakosci.com) ，非常好更新，使我的张量升维。

General regression neural network，维基百科：General regression neural network – Wikipedia

本篇涵盖了广义回归神经网络的原理及其推导，其神经网络的构建，并根据其高度可并行化的特征，使用了Pytorch来构建算法，利用GPU来加速算法的运行。

课题项目的缘故开始接触这个算法，但似乎找不到哪个包里有能直接调用的实现？不过反正也不是很复杂，直接来动手实现好啦。先根据论文^[1]整理一下算法的原理和我的推导思路：

假定当前存在一个已知的联合概率密度函数（probability density function，后文简称pdf）：\(f\left (x,y \right)\)，其中\(x\)代表一个随机向量，\(y\)则代表一个标量的随机变量，现在的问题是：在\(x\)为特定值\(X\)的条件下，\(y\)的期望是多少？即求条件期望\(E\left [y|X \right]\)。

先上一个条件概率公式：$$f_{y|X}(y|X)=\frac{f(X,y)}{f_{X}(X)}\cdots (1)$$
其中\(f_{y|X}\)是条件概率密度，\(f\)是最开始说的pdf，而\(f_{X}\)则代表向量\(x\)的概率密度。

现在开始展开条件期望：$$E[y|X]=\int_{-\infty}^{\infty}yf_{y|X}(y|X)\mathrm{d}y$$于是根据公式(1)：$$=\int_{-\infty}^{\infty}\frac{yf(X,y)}{f_{X}(X)}\mathrm{d}y=\frac{\int_{-\infty}^{\infty}yf(X,y)\mathrm{d}y}{f_{X}(X)}$$最终得到：$$E[y|X]=\frac{\int_{-\infty}^{\infty}yf(X,y)\mathrm{d}y}{\int_{-\infty}^{\infty}f(X,y)\mathrm{d}y}\cdots (2)$$

现在我们把目光放在求\(f(X,y)\)上来，于是正式进入GRNN算法的核心内容之——高斯函数，并将样本引入到算法中，利用样本来估计概率密度。设\(x\)和\(y\)的已知样本为\(X^{i}\)和\(Y^{i}\)，\(i=1,2,\dots,n\)，\(n\)是样本数量，设\(p\)为向量\(x\)的维数，下面我将给出一串又臭又长)-:的公式：
$$\hat{f}(X,y)=\frac{1}{n}\sum_{i=1}^{n}\prod_{j=1}^{p}[\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(X_j-X_j^i)^2}{2\sigma^2})]\cdot\frac{1}{\sqrt{2\pi}}exp(-\frac{(Y-Y^i)^2}{2\sigma^2})$$
$$=\frac{1}{(2\pi)^{\frac{(p+1)}{2}}\sigma^{(p+1)}}\frac{1}{n}\sum_{i=1}^{n}exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\cdots (3)$$
仔细看就会明白，公式(3)实际上做的事情就是先构建\(p+1\)维的联合高斯分布，\(p\)维来自\(x\)而加上的一个维度就是\(y\)。接着根据\(n\)个样本生成了\(n\)个高斯分布，取对应样本的值作为每个高斯分布的均值\(\mu\)，但方差\(\sigma\)统一，实际上这个方差将是GRNN唯一的超参数，也可以称为平滑参数。最后将这\(n\)个高斯分布加起来再除以\(n\)，以保证生成的概率密度函数在整个空间上的积分为1。

上面这一步其实很容易理解，想象在经典的二维坐标系中，x轴上有许多点，以每一个点为中心构建方差一致的正态分布，并加在一起再除以点的个数，就得到了一个概率密度函数。最终在x轴上的点密集的地方概率密度就高，点稀疏的地方概率密度就低，而一开始统一的方差则决定了最终图像的形状，方差高则概率密度更均匀，起伏更缓，反之则更陡，故称平滑参数。于是根据得到的概率密度函数，我们就能够估计新来的点落在x轴某个位置的概率是多少。（从这里也能看出喂给GRNN的训练样本一定要覆盖的情况够全面，该算法在缺乏训练的空间上几乎没有预测能力:-）

得到概率密度\(f(X,y)\)的估计之后，就可以回到公式(2)，开始计算条件期望了，此时公式(2)改成如下形式：$$\hat{Y}(X)=\frac{\int_{-\infty}^{\infty}y\hat{f}(X,y)\mathrm{d}y}{\int_{-\infty}^{\infty}\hat{f}(X,y)\mathrm{d}y}$$
带入公式(3)，消去系数：$$=\frac{\int_{-\infty}^{\infty}y\sum_{i=1}^{n}exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y}{\int_{-\infty}^{\infty}\sum_{i=1}^{n}exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y}$$
求和的积分等于积分的求和：$$=\frac{\sum_{i=1}^{n}\int_{-\infty}^{\infty}y\cdot exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y}{\sum_{i=1}^{n}\int_{-\infty}^{\infty}exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y}$$
$$=\frac{\sum_{i=1}^{n}exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})\int_{-\infty}^{\infty}y\cdot exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y}{\sum_{i=1}^{n}exp(-\frac{(X-X^i)^{T}(X-X^i)}{2\sigma^2})\int_{-\infty}^{\infty}exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y}$$
现在对公式分子分母后方的积分式子进行化简，具体方法就是构造高斯函数：
$$\int_{-\infty}^{\infty}exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y=\sqrt{2\pi}\sigma\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y=\sqrt{2\pi}\sigma$$
$$\int_{-\infty}^{\infty}y\cdot exp(-\frac{(Y-Y^i)^2}{2\sigma^2})\mathrm{d}y=\sqrt{2\pi}\sigma\int_{-\infty}^{\infty}y\cdot N(Y^i,\sigma^2)\mathrm{d}y=\sqrt{2\pi}\sigma\cdot Y^i$$
计算即将完成，这里我们先设\(D_i^2=(X-X^i)^{T}(X-X^i)\)，即测试样本\(X\)与每个训练样本之间欧氏距离的平方。
最终得到了GRNN的公式：$$\hat{Y}(X)=\frac{\sum_{i=1}^{n}Y^{i}exp(-\frac{D_i^2}{2\sigma^2})}{\sum_{i=1}^{n}exp(-\frac{D_i^2}{2\sigma^2})}\cdots (4)$$

所以说GRNN实际上是一个只有前向传播的统计学习方法……而因为没有需要被迭代优化的参数，它的训练过程只有接收训练样本这一步骤而已，反而在预测时测试样本需要跟每一个训练样本发生作用，耗时集中在预测这一步骤。然后你可能会注意到，似乎上面的计算中\(y\)一直都是一个标量，那如果遇到多个输出维度的情况该怎么办？当然是每个输出维度单独作为一次计算，接下来的神经网络构建部分也是综合了多维度输出的情况（具体表现在求和层）。

算法的原理和推导以上就是全部了，接下来需要将公式(4)转化为神经网络的形式，不过这里就不画神经网络的示意图了，直接用矩阵的形式表达。将构建一个具有高斯层、求和层和输出层的神经网络，其中求和层与输出层将在具体实现中合并为一个层。

高斯层（即\(exp(-\frac{D_i^2}{2\sigma^2})\)）：
设向量\(x\)为测试输入样本，矩阵\(t\)为训练输入样本集合，每一个输入样本的维度均为\(p\)，一共有\(n\)个训练样本，Gauss即公式\(exp(-\frac{D_i^2}{2\sigma^2})\)，即令测试输入样本与每个训练输入样本经过一次计算，得到行向量\(g\)，流程图：

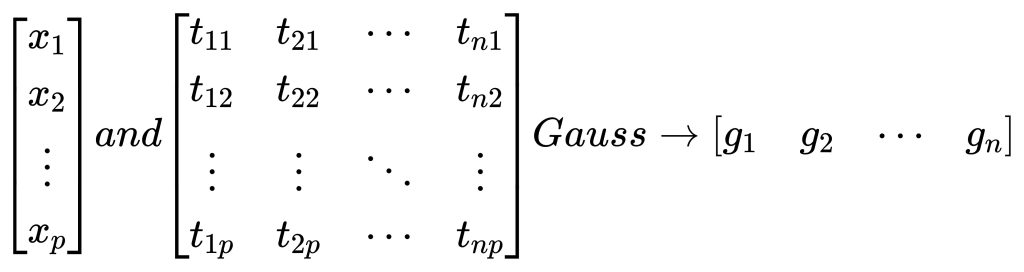
其pytorch类代码实现如下：

class GaussLayer(nn.Module):
    def __init__(self, training_inputs, sigma):
        super(GaussLayer, self).__init__()
        self.training_inputs = training_inputs
        self.sigma = sigma  # smoothing parameter

    def forward(self, x):
        out = x - self.training_inputs
        out = (out ** 2).sum(axis=1)
        out = - out / (2 * self.sigma ** 2)
        out = torch.exp(out)
        return out

求和与输出层：
向量\(g\)自身求和得到\(s_0\)，对应公式(4)的分母：

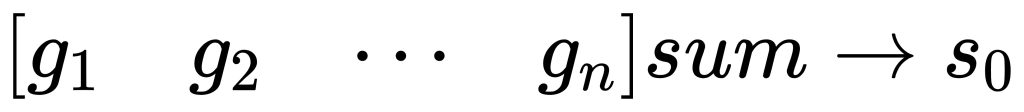
训练输出样本\(y\)同样写成矩阵的形式，其中\(k\)代表单个输出样本的维度。行向量\(g\)与矩阵\(y\)的每一行经过求和层\(Sum\)进行一次内积，得到向量\(s\)，向量\(s\)再除以前面求得的\(s_0\)，最终得到预测输出向量\(o\)，流程图：

其pytorch类代码实现如下：

class SumAndOutputLayer(nn.Module):
    def __init__(self, training_outputs):
        super(SumAndOutputLayer, self).__init__()
        self.training_outputs = training_outputs

    def forward(self, x):
        trans = self.training_outputs.T
        s0 = x.sum()
        out = (x * trans).sum(axis=1)  # Summation Layer
        out = out / s0  # Output Layer
        return out

可以看到，矩阵化后的流程中，绝大部分步骤都符合Pytorch的广播机制，因此非常适合通过自定义层来实现其整个运算过程、再将模型和数据放在GPU上运行，可以极大地改善GRNN在预测时的耗时问题。

下面将给出完整的代码，其中GRNN类中包含了数据归一化和还原的步骤。

需要注意的是，pytorch实现中使用的变量类型与上文所使用的向量、矩阵的结构有所差异。文中不论是列向量还是行向量，在代码中均表现为一维张量；矩阵用二维张量表示，文中每列代表一个样本，但代码中每行代表一个样本；而注意超参\(\sigma\)在调用类之前也需要先转化为零维张量。再者，当训练输入样本或训练输出样本（特别是输出常有这种情况）为一维，所有样本放在一个一维张量下时，必须先使用a = a.unsqueeze(axis=1)进行升维。

import torch
from torch import nn


class GaussLayer(nn.Module):
    def __init__(self, training_inputs, sigma):
        super(GaussLayer, self).__init__()
        self.training_inputs = training_inputs
        self.sigma = sigma  # smoothing parameter

    def forward(self, x):
        out = x - self.training_inputs
        out = (out ** 2).sum(axis=1)
        out = - out / (2 * self.sigma ** 2)
        out = torch.exp(out)
        return out


class SumAndOutputLayer(nn.Module):
    def __init__(self, training_outputs):
        super(SumAndOutputLayer, self).__init__()
        self.training_outputs = training_outputs

    def forward(self, x):
        trans = self.training_outputs.T
        s0 = x.sum()
        out = (x * trans).sum(axis=1)  # Summation Layer
        out = out / s0  # Output Layer
        return out


class CudaGeneralRegNN:
    def __init__(self):
        self.t = None  # training samples (INPUT)
        self.y = None  # training samples (OUTPUT)
        self.sigma = None  # smoothing parameter
        self.t_mean = None  # mean of each feature (INPUT)
        self.t_std = None  # std of each feature (INPUT)
        self.y_mean = None  # mean of each feature (OUTPUT)
        self.y_std = None  # std of each feature (OUTPUT)
        self.net = None  # General Regression Neural Network
        self.device = None  # cpu/cuda

    def fit(self, t_samples, y_samples, sigma):
        self.device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
        self.t = t_samples
        self.y = y_samples
        self.sigma = sigma
        self.t_mean = self.t.mean(axis=0)
        self.t_std = self.t.std(axis=0)
        self.y_mean = self.y.mean(axis=0)
        self.y_std = self.y.std(axis=0)

        # Normalization
        self.t = (self.t - self.t_mean) / self.t_std
        self.y = (self.y - self.y_mean) / self.y_std

        self.t = self.t.to(device=self.device)
        self.y = self.y.to(device=self.device)
        self.sigma = self.sigma.to(device=self.device)

        self.net = nn.Sequential(
            GaussLayer(self.t, self.sigma),
            SumAndOutputLayer(self.y)
        )
        self.net = self.net.to(device=self.device)

    def predict(self, x):
        x = (x - self.t_mean) / self.t_std
        x = x.to(device=self.device)

        out = self.net(x)

        out = out.to(device=torch.device('cpu'))
        out = out * self.y_std + self.y_mean

        return out

耶整理完了，其实论文^[1]只给出了一些比较粗略的公式，很多部分是我自己推导的，疲れた…

参考文献：
[1]D. F. Specht, “A general regression neural network,” in IEEE Transactions on Neural Networks, vol. 2, no. 6, pp. 568-576, Nov. 1991, doi: 10.1109/72.97934.